

4 Sectionally Rational- and Rows of Delta Functions 28 1. Oregon State University Corvallis, Oregon Eastern Michigan University Ypsilanti, Michigan The Authors Contents Part I. Jolan Eross for her tireless effort and patience while typing this manu script. Latin letters denote (unless otherwise stated) real positive parameters and a possible extension to complex values by analytic continuation will often pose no serious problem. Greek letters denote complex parameters within the given range of validity. Special consideration is given to results involving higher functions as integrand and it is believed that a substantial amount of them is presented here for the first time. Erdelyi and Roberts and Kaufmann (see References). Previous publications include the contributions by A. The usef- ness of this kind of information as a tool in various branches of Mathematics is firmly established. Note that for β = 1 g( t) = d( t − 1), a Dirac delta function which is represented as a vertical line in figure 1c.This material represents a collection of integrals of the Laplace- and inverse Laplace Transform type. Figures 1a 1a – c contain graphs of g( t) as a function of t over the entire range of tabulated values of β.
LAPLACE TRANSFORM TABLE SERIES
For example, if β=0.6 the sum of seven terms of the series gives g(10) to six places, and the sum of four terms gives g(100) to the same accuracy. There is little need to tabulate g( t) for t > 5 because for these values, the sum of no more than 10 terms of the series in eq (5) suffice to produce g( t) to six-digit accuracy for values of β in the interval (0.05,0.999). Additional Physical Format: Online version: Oberhettinger, Fritz. Spacings in t vary with β and t in such a way that the peaks of g( t) are most densely covered. The finer intervals in β at low values of β are required because of the considerable changes in the function in that neighborhood. Tables, Graphs, and Numerical Approximations This has been particularly encouraged by the observation that nearly all glassy relaxation phenomena can be described by the Kohlrausch-Williams-Watts (KWW) functionģ. X(s) x( Table 2.2.1 (Continued) x(), t 0 X(s Table 2.2.2 Properties of the.

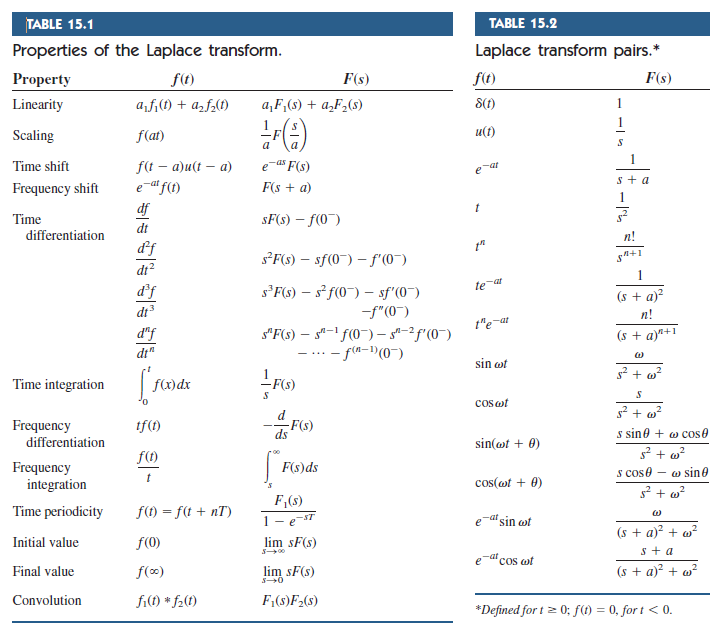
In recent years theorists have become interested in the possibility that complex disordered systems exhibit universal features in their relaxation and transport properties, possibly arising from self-similar arrangements of obstacles to motion. This problem has been solved Table 2.2.1 Table of Laplace transform pairs.
It is also seen in measurements of volumetric, and thermal response. This is especially clear from measurements obtained from mechanical, dielectric, and photon correlation spectroscopy. It is also now generally recognized that all glassy materials exhibit non-exponential relaxation behavior both above and below the glass transition temperature, T g. It has been known for at least 150 years that mechanical relaxation in solids is non-exponential, the decay often being characterized by a fractional power-law or logarithmic function.


 0 kommentar(er)
0 kommentar(er)
